Станислав Ежи Лец
Интерес к астрономии в Карелии растет, неслучайно материалы этой серии лидируют по числу просмотров в нашем педагогическом вестнике. В этом выпуске решения к задачам 9 класса и задание для десятиклассников.
Решения заданий для 9 класса
9.1. Кратеры на ВенереНа фото вы видите кратеры на Венере. Когда измерили глубину кратеров на Венере, оказалось, что они менее глубоки, чем кратеры на Луне. Почему?
РЕШЕНИЕ: У Венеры в отличие от Луны есть атмосфера, так что метеориты в атмосфере из-за сопротивления венерианского «воздуха» заметно теряют свою скорость. Удар о поверхность получается слабее, и глубина кратера, который получается в результате удара, поэтому меньше.
|
|
|
|
9.2. Великолепная восьмеркаНа фото представлен хорошо вам известный космический объект, снятый с земной поверхности. 1. Что это за объект? РЕШЕНИЕ. На фотографии 36 изображений Солнца, снятые в разные дни года в одно и то же время суток, при этом фотокамера не меняла своего положения. Если бы движение Солнца по небесной сфере было равномерным, то изображения располагались бы по дуге окружности (например, при съемке в 12.00 местного времени Солнце было бы видно строго на юге на разной высоте). Поскольку движение Солнца неравномерно, его положения в одно и то же время суток немного смещены, и вместо дуги окружности получается восьмерка. Такая кривая (положение Солнца в одно и то же время суток в разные дни года) называется аналема.
|
9.3. Почти по «Гарри Поттеру»
Заметка из газеты («Арт-мозаика», № 10–2001): «В прошлом году дорожный патруль штата Аризона обнаружил металлическую конструкцию, впечатавшуюся в скалу на высоте 50 футов. Картина напоминала авиакатастрофу, однако эксперты выяснили, что средство передвижения до встречи со скалой было автомобилем Шевроле.
Хозяин машины где-то раздобыл брикет твердого ракетного топлива и решил побаловать железного друга. Выехав в пустыню, нашел прямой и длинный участок шоссе, присобачил к машине капсулу с брикетом, слегка разогнался и поджег брикет.
Дальше все было как в сказке: видели добра молодца севши, не видели поехавши. Всё остальное эксперты установили с известной долей вероятности – по характеру горения и плавления асфальта и другим косвенным данным. Место старта находилось более чем в трех милях от финиша, то есть от скалы. Несчастная «Антилопа Гну» развила скорость около 350 миль в час и оставалась на дороге на протяжении двух с половиной миль (10-15 секунд). Водитель при этом испытал перегрузки, более типичные для авиации, но все еще пытался затормозить, в результате шины стерлись, оставив на дороге жирный черный след. Затем машина, конечно, взлетела и оставшуюся до скалы милю преодолела по воздуху…»
Представьте себе, что вы как раз тот специалист-эксперт, которому поручили разобраться в причинах катастрофы.
1) Для начала объясните, почему машина взлетела.
2) Оцените, какой скорости должна была достигнуть машина для взлета.
РЕШЕНИЕ. Корпус машины вместе с ее днищем можно считать своеобразным крылом, так что при движении машины обязательно возникает подъемная сила. Обычно машины не взлетают, потому что предусмотренная (и записанная в паспорте) максимальная скорость дает подъемную силу, намного меньшую, чем вес машины.
Хозяин машины, можно сказать, обеспечил ее авиационным реактивным двигателем, так что она достигла авиационных скоростей и подъемная сила превысила силу тяжести.
Грубо оценить критическую скорость можно, применив уравнение Бернулли: за счет движения обтекающего корпус машины потока воздуха возникнет перепад давлений, направленный вверх:
ΔP=ρv2/2 (1)
Тогда подъемную силу можно оценить по формуле
F= ΔP∙`S (2),
где S – площадь днища.
Чтобы машина взлетела, подъемная сила должна сравняться с силой тяжести:
F=mg (3).
Подставляя (1) и (2) в (3), получим
ρSv2/2 =mg,
откуда
v2= 2mg/ρS .
Тогда, подставляя плотность воздуха ρ≈1,3кг/м3 , площадь днища S≈2,5м2, масса автомобиля m ≈ 1200кг, g ≈10м/с2, получим v ≈ 90м/с ≈ 324км/час.
Современные гоночные автомобили могут иметь такие скорости, но они не взлетают, поскольку оснащены антикрылом – поверхностью, которая расположена так, что аэродинамическая сила со стороны встречного потока воздуха прижимает машину к трассе и потому компенсирует подъемную силу.
9.4. Остановись, затменье, ты прекрасно!
Известно, что полная фаза солнечного затмения продолжается 2-7 минут. Предложите способ продлить наблюдение.
РЕШЕНИЕ. Как продлить наблюдение? Область затмения представляет собой тень от Луны, которая движется по поверхности Земли. Можно попытаться догнать затмение – из точки, откуда затмение ушло, переместиться в точку, где полная фаза затмения еще идет.
Хватит ли для этого скорости? Известно, что, например, во время затмения 11 августа 1999 г. в южной Англии полное затмение наблюдалось около 10.30 по Киевскому времени, а в Венгрии – в 12.30. Расстояние от Лондона до Будапешта – около 1500 км. Необходимая скорость (750 км/ч) доступна пассажирскому реактивному самолету.
Значит, для того чтобы наблюдать затмение подольше, нужно сесть на реактивный самолет и лететь вслед за тенью от Луны. Такие экспедиции осуществлялись в действительности.
9.5. Незнакомая планета
Подлетев к незнакомой планете, космический корабль перешел на низкую круговую орбиту. Смогут ли космонавты, пользуясь только часами, определить среднюю плотность вещества планеты? Как?
Напоминаем на всякий случай, что объем шара радиуса R вычисляется по формуле
V = 4πR3/3
РЕШЕНИЕ. Корабль обращается по низкой орбите (радиус орбиты равен радиусу R планеты) с периодом T под действием гравитационной силы. Запишем второй закон Ньютона для корабля:
Средняя плотность планеты
Из формулы (1) получаем:
Откуда
9.6. В открытом космосе
Космонавт массы m1 приближается к космическому кораблю массы m2 с помощью легкого троса. Первоначально корабль и космонавт неподвижны, а расстояние между ними равно L. Какое расстояние пройдет космонавт до встречи с кораблем?
РЕШЕНИЕ. Система «Космонавт-трос-корабль» замкнутая. Следовательно, ее центр масс должен иметь постоянную скорость. Поскольку вначале все тела неподвижны, то центр масс системы неподвижен. Следовательно, космонавт и корабль встретится в центре масс системы. Найдем, на каком расстоянии от космонавта он находится. Примем первоначальное положение космонавта за начало координат. Тогда начальная координата корабля равна L. Найдем координату центра масс:
Поскольку эта координата отсчитывается от начального положения космонавта, именно такое расстояние пройдет космонавт до встречи с кораблем.
Этот же ответ можно получить, применив закон сохранения импульса.
Задания для 10 класса
10.1. Великолепная восьмерка
(см. задание 9.2 для 9-го класса)
10. 2. «Черный – это цвет?»
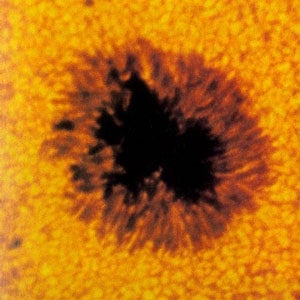
На фотографии вы видите солнечное пятно на поверхности Солнца. Как вы догадываетесь, вещество поверхности Солнца представляет собой раскаленный газ, именно этот газ и дает солнечный свет, потому поверхность Солнца называется фотосфера. Почему же пятно черное?
10.3. Вакуум в телескопе
У некоторых солнечных телескопов из трубы выкачан воздух. Для чего это сделано?
10. 4. Льдина в небе?
Заметка из газеты: «Во время полета на космической станции «Салют» советский космонавт Георгий Гречко обнаружил на одной из фотографий… льдину, висящую в воздухе выше облаков! Только на Земле удалось разобраться в этом странном явлении…»
Как могла получиться такая фотография? Предложите свое объяснение.
10.5. Нагреть Шелезяку
Планета Шелезяка очень похожа на Землю, но на последних выборах во Всемирный Парламент там победили антиэкологисты, которые немедленно построили на всей поверхности планеты (включая моря и океаны) атомные электростанции для нагрева атмосферы. На один квадратный метр поверхности Шелезяки приходится тепловая мощность 100 Вт. Через какое время температура атмосферы увеличится на 10оС? Считайте, что сама планета не нагревается, а мощность излучения в космос остается неизменной.
10.6. Как взвесить Галактику?
Оценки массы Галактики, полученные разными способами, дают разные результаты. Визуальный способ состоит в том, что подсчитывают массу светящегося вещества Галактики, расположенного в пределах трех миллиардов астрономических единиц от центра Галактики (r=3∙109a.e.). Такой подсчет показывает, что в этих пределах сосредоточена масса М1=1,5•1011МС (МС=2•1030кг – масса Солнца).
Астрономическая единица (а.е) – среднее расстояние от Земли до Солнца.1а.е.=1,5•1011м
С другой стороны, измерено, что звезды, находящиеся на расстоянии r=3•109 a.e.от центра, обращаются вокруг центра с периодом Т=3,75•108лет, и по этим данным вычисляют другое значение М2 массы нашей Галактики.
Определите величину расхождения и попытайтесь объяснить, какими причинами это расхождение вызвано.