Приемы работы над определением

Многие школьники заучивают определения механически и, соответственно, не умеют их использовать. Решение проблемы предложено в этой статье.

Аннотация

Эта статья поможет учителю начальных классов и учителю-предметнику организовать в классе работу над определением. Педагоги получат возможность освоить и использовать на уроках алгоритмы построения определений, работы над готовым определением, создания контрпримеров и задач-ловушек. Завуч может применить этот материал в рамках организации методической работы над проблемой формирования познавательных УУД. Наконец, старшеклассники вполне могут освоить представленные здесь алгоритмы самостоятельно, а родители более младших учеников — использовать их для помощи детям в учебной деятельности.

Несколько лет назад в одном из вузов на экзамене по биологии произошел курьезный случай. На вопрос «Что делают белки в клетке?» ученик, удивленный столь странным, по его мнению, для данной ситуации вопросом, тем не менее достаточно подробно описал поведение посаженной в клетку белочки: как она крутится в колесе, лузгает орешки, карабкается по решеткам.  Удивленная комиссия (которая имела в виду не белку, а белок – одно из важнейших для организма химических соединений) в свою очередь задумалась о корректности вопроса… Не знаем, чем закончилась эта история, но ситуация, в которой ученик понимает под словом совсем не то (или не совсем то), что имелось в виду в учебнике, встречается достаточно часто.

В каждом учебном предмете есть свой понятийный аппарат, и с определениями понятий дети сталкиваются с первого класса. С каждым годом понятий становится все больше, однако многие школьники заучивают определения механически и, соответственно, не умеют их использовать.

Подход к работе с понятийным аппаратом подробно разработан российским психологом Н.Ф. Талызиной. В этой статье мы показываем приемы реализации этого подхода, основанные на инструментах ОТСМ-ТРИЗ, которые эффективно используются в различных учебных курсах. Начать работу целесообразно  уже в третьем классе начальной школы. В нашем опыте алгоритм построения определений вводился в курсе развития творческого воображения на базе ТРИЗ, однако аналогичную работу можно провести в рамках любого предмета. Последовательность действий учителя будет выглядеть следующим образом.

1. Организуется работа над изучением признаков различных объектов. В ОТСМ-ТРИЗ педагогике используются игровые тренинги и модель «Элемент – Имена признаков – Значения признаков».  Понятия «часть»,  «место» вводятся как признаки объектов наравне с другими понятиями[1].

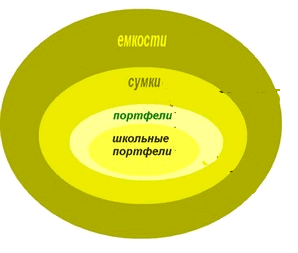
2. Вводится модель вложенных множеств (круги Эйлера, диаграммы Венна – рис. 1), отражающая родовидовые отношения.

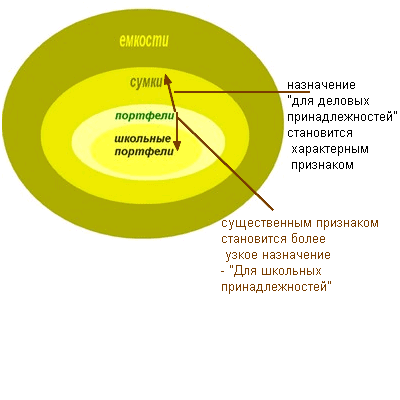
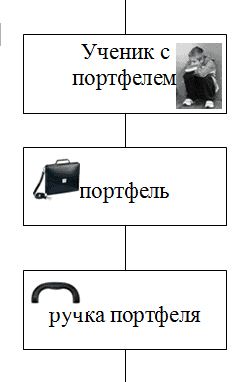
3. Параллельно с моделью вложенных множеств используется модель «системного лифта» (рис. 2). Если в первом случае модель отражает родовидовые отношения, то во втором – структуру объекта (сравните фрагменты двух определений: 1) автомобиль – транспортное средство… и 2) колесо – часть транспортного средства…

4. На основе вложенных множеств дается понятие:

— существенного признака 1) как признака, собирающего объекты в данную группу (существенный признак – тот, без которого объекты данной группы НЕ СУЩЕСТВУЮТ, становятся чем-то другим); 2) как признака, значения которого для данной группы объектов не меняются;

— характерного признака, по значению которого объекты в данной группе могут отличаться.

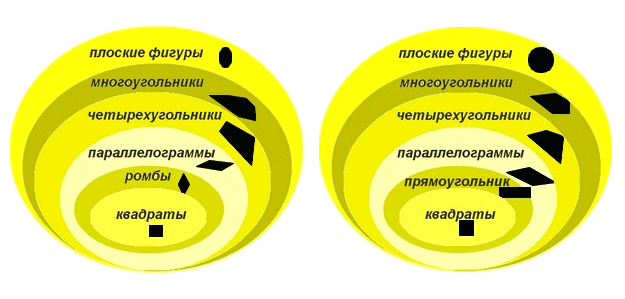
Так группа «многоугольники» собрана по существенным признакам «замкнутая», «ломаная», а количество углов является характерным признаком конкретного многоугольника.

5. Отрабатываются переходы по вложенным множествам: чтобы перейти к внутреннему множеству (к подгруппе), надо зафиксировать (сделать постоянным, а, значит, существенным) значение одного или нескольких характерных признаков и наоборот, переход к внешнему множеству предполагает переход от фиксированных значений признаков к их спектрам (существенные признаки во внешнем множестве превращаются в характерные). Например, для объекта из множества квадратов существенные признаки – плоская фигура, замкнутая ломаная, 4 угла (стороны), прямые углы, равные стороны. Для объекта из внешнего множества прямоугольников равные стороны уже не будут существенным признаком. Теперь это характерный признак некоторых прямоугольников, тех, что являются квадратами.

В курсе РТВ (а при его отсутствии – на других уроках) предусмотрены тренинги, позволяющие по-разному определять один и тот же объект через различные внешние группы (множества). Так, квадрат можно «достать» из внешнего множества «прямоугольники», а можно – из множества «ромбы» (рис. 3).

Квадрат – это прямоугольник, у которого все стороны равны (описание квадрата через внешнее множество «прямоугольники»);

Квадрат – это ромб, у которого все углы прямые (описание квадрата через внешнее множество «ромбы»). Аналогичная работа проводится для различных видов объектов (рис. 4).

5. Уточняются отличительные признаки, используемые в тренингах (в каждой конкретной ситуации это: либо подсистемы, либо свойства, либо связи, либо причины или следствия (для процесса, явления), т.е. понятия, освоенные учащимися при изучении элементов ТРИЗ.

6. Выявляются существенные признаки (для технических систем за существенный признак обычно принимается функция), именно они используются при построении вложенных множеств.

Осваивается схема построения определения:

<объект> –

это

< надсистемная группа> или <надсистема по месту>,

отличающаяся тем, что:

<отличительные существенные признаки>.

В дальнейшем на других уроках применяются следующие виды работ:

— построение определения детьми на основе эмпирического опыта и работа на основе построенного определения – алгоритм 1;

— введение определения учителем и работа по готовому определению (в случаях, когда вводится абстрактное понятие и опереться на опыт детей невозможно) – алгоритм 2.

— составление контрпримеров и задач-ловушек – алгоритм 3.

Алгоритм 1. Построение определения детьми

1. Вводится копилка объектов (множество объектов, подходящих под определение или более широкое множество).

Копилка может быть дана учащимся в готовом виде, либо представлена частично, с тем, чтобы дети дополнили ее, либо собрана детьми на основе эмпирического представления об объекте, который мы собираемся определить.

Так, перед определением биссектрисы в треугольнике просим учеников изобразить треугольники и провести биссектрисы. С понятием биссектрисы угла дети знакомы.

2. Анализ копилки. Выделение спектра объектов, подходящих под задуманное определение.

Учитель выбирает те чертежи, где изображена именно биссектриса треугольника.

3. Построение вложенных множеств. В процессе построения необходимо выявить группу (внешнее множество) и найти те признаки, которые отличают некоторые объекты данной группы от других, входящих в ту же группу. Часто полезно параллельно с вложенными множествами построить системный лифт. На этом этапе происходит тщательное выявление свойств объекта.

Внешняя группа для биссектрисы треугольника – отрезки. Надсистема в системном лифте – биссектриса угла.

4. Построение определения по схеме 1.

Биссектриса треугольника – это отрезок, который выходит из вершины, оканчивается на стороне и делит угол пополам.

Или: Биссектриса треугольника – это часть биссектрисы угла, лежащая внутри треугольника.

5. Проверка определения (поиск контрпримеров). Поиск объекта, который подходит под определение, но не является определяемым объектом. При необходимости – корректировка определения.

Контрпримеры покажут, что второй вариант определения неточен. Уточним: «… – все точки биссектрисы угла, лежащие внутри треугольника».

6. Далее проводится работа по анализу определения (алгоритм 2 от пункта 3 ).

Алгоритм 2. Работа над готовым определением

1. Выявление главных признаков (определение пишется на доске, обсуждается, какие слова нельзя выбросить из определения и почему).

2. Определение переписывается в схему 1.

3. «Раскрутка» определения (сделать все признаки «открытыми», дать явное определение всем признакам, встречающимся в данной формулировке). В случае с биссектрисой стоит обратить внимание на понятие «отрезок».

4. Собирается копилка объектов по определению (дополнение исходной копилки). Варьируя несущественные признаки, получают спектр примеров. В нашем случае – биссектрисы в разных видах треугольников.

5. Выявляются границы применимости определения. В случае с биссектрисой все должно происходить на плоскости.

6. Следующим этапом работы является построение контрпримеров и основанных на них задач-ловушек. Преимущество «ловушек» состоит в том, что они позволяют свести к наглядному противоречию ошибки, возникающие вследствие небрежного обращения с определением. С их помощью мы можем многократно возвращаться к данному материалу, не снижая мотивации его изучения. Учитель предлагает классу готовые «ловушки» и просит построить собственные (по заданному алгоритму).

Алгоритм 3. Построение контрпримеров и задач-ловушек

1. Записать определение в виде, показанном на схеме 1.

2. Удалить 1 признак или заменить внешнюю группу. Например, биссектриса – не отрезок, а просто линия.

3. Найти объект, подходящий под получившееся определение. Вместо отрезка биссектрисы в треугольнике кривая, симметричная относительно биссектрисы.

4. Выявить свойства, которые исчезают или меняются вместе с измененным признаком или заменой группы. В нашем случае перестает определяться однозначно длина биссектрисы.

5. Построить противоречие с этими свойствами. В зависимости от специфики объекта противоречие строится:

— аналогично методу «от противного» в математике (выявляя свойства объекта, полученного в контрпримере, получаем свойство, которого не может быть),

— либо демонстрируется противоречие с опытом детей (в треугольнике изучают обычно «ровные» линии, а тут выходит, что по определению линия может быть и кривой),

— либо с фактом (длина линии может быть разной, а в ответе дана одна конкретная длина).

Выводы

Алгоритмы работы с определениями межпредметны. Они могут быть введены при изучении любой школьной дисциплины и являются простыми и эффективными инструментом, который целесообразно использовать в различных учебных курсах.

Самостоятельное построение учащимися определений, анализ готовых определений и синтез задач-ловушек позволяют формировать универсальное учебное действие «подведение под понятие» и обеспечивают осознанное критическое отношение учеников к понятийному аппарату в изучаемой области знаний.

Литература

Талызина Н. Ф. Педагогическая психология: Учеб. пособие для студ. сред. пед. учеб. заведений. — М.: Издательский центр «Академия», 1998. — 288 с.