
Если бы мы познали все тайны Вселенной, мы тотчас впали бы в неизлечимую скуку.
А. Франс
Эта публикация завершает «Космическую Одиссею» — самый читаемый материал журнала «Полёт» в этом году.
Ответы на задания для 11 класса
11.1. Великолепная восьмерка
На фото представлен хорошо вам известный космический объект, снятый с земной поверхности.
1. Что это за объект?
2. Как проводились съемки?
3. Почему на фото получилась «восьмерка»?
РЕШЕНИЕ. На фотографии 36 изображений Солнца, снятые в разные дни года в одно и то же время суток, при этом фотокамера не меняла своего положения. Если бы движение Солнца по небесной сфере было равномерным, то изображения располагались бы по дуге окружности (например, при съемке в 12.00 местного времени Солнце было бы видно строго на юге на разной высоте). Поскольку движение Солнца неравномерно, его положения в одно и то же время суток немного смещены, и вместо дуги окружности получается восьмерка. Такая кривая (положение Солнца в одно и то же время суток в разные дни года) называется аналема.
11.2. Куда девались кольца?

Вы, конечно, узнали на фото планету Сатурн по его знаменитым кольцам. Но однажды Сатурн поразил наблюдателей: наведя телескоп на Сатурн, они не увидели колец! Как бы вы объяснили этот поразительный факт?
РЕШЕНИЕ. Если вы смотрите на 100-долларовую купюру, обращенную к вам портретом, то видите ее хорошо. Если ту же купюру расположить к вам ребром на уровне глаз, вы ее скорее всего не заметите даже с очень близкого расстояния.
Кольца Сатурна, имея большую ширину (по ширине кольца могло бы разместиться несколько земных шаров), имеют очень малую по астрономическим меркам толщину — всего несколько километров. Когда кольца поворачиваются к наблюдателю ребром, их можно заметить только в очень сильные телескопы как яркую полоску.
11.3 Блуждающие зонды
Одно время в качестве спутников-ретрансляторов попробовали использовать надувные зонды (шары радиусом около 50 метров). Через несколько месяцев выяснилось, что все зонды ушли с расчетных орбит. Как вы думаете, по какой причине?
Оцените силу, которая «сносила» зонды.
РЕШЕНИЕ. Зонды уходили с орбит под действием силы светового давления со стороны Солнца.
Оценить ее можно, вспомнив известную формулу для мощности
N=Fv.
В нашем случае N –мощность солнечного излучения, падающего на шар, v=с – скорость света. Тогда сила светового давления
F=N/с
Мощность излучения, падающего на шар вблизи земной орбиты можно оценить, зная солнечную постоянную
α=N/S=1,4∙103 Вт/м2
Тогда
F= α S/с= απR2/c
Подставляя численные данные, получим F≈3,5 Н.
11.4 Улыбка без кота
Астроном-любитель Арчер Салли наблюдал комету, которая не имела ядра, а имела только один хвост. Он назвал ее «чеширской кометой» по аналогии с Чеширским котом, который исчезал, а улыбка его еще оставалась.
Объясните, как могла получиться комета без ядра.
РЕШЕНИЕ. Ядро кометы к моменту наблюдения полностью испарилось. Кстати, хвост у кометы появляется как раз благодаря испарению ядра.
11.5 Космические часы
Некоторые звезды пульсируют, причем период этих пульсаций для каждой звезды постоянен. Выведите формулу для этого периода, если известны масса и радиус звезды. Оцените период пульсаций численно для звезды с параметрами, близкими к параметрам Солнца.
РЕШЕНИЕ.
Выведем формулу периода пульсаций по аналогии, сравнивая пульсации звезды с колебаниями математического маятника.
Период маятника
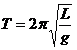 (1),
(1),
где L-длина маятника, g – ускорение свободного падения.
Для пульсаций звезды линейным параметром L-будем считать радиус звезды (L =R), а ускорение свободного падения на поверхности звезды найдем из закона всемирного тяготения:
g=GM/R2 (2)
Тогда формула (1) примет вид
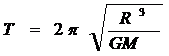
Для звезды с параметрами Солнца М=2∙1030кг и R =7∙108м получаем период пульсаций
Т≈104с=2,8 часа.
11.6. Улететь безвозвратно
Метеорит на очень большом расстоянии от планеты имеет скорость v0, падая на нее, он имеет скорость v. Какую скорость нужно сообщить космическому кораблю на поверхности планеты, чтобы он покинул ее безвозвратно.
Решение. Пусть радиус планеты равен R, а ее масса равна М. Тогда на большом расстоянии от планеты полная энергия метеорита равна его кинетической энергии в тот момент:
![]() .
.
В момент падения на планету его энергия складывается из кинетической энергии и потенциальной энергии притяжения к планете:
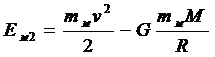 .
.
По закону сохранения энергии
![]() ,
,
Откуда
![]() . (*)
. (*)
Чтобы корабль покинул планету безвозвратно, ему нужно сообщить вторую космическую скорость vк – такую, чтобы его кинетическая энергия по модулю равнялась потенциальной энергии его притяжения к планете:
![]() ,
,
откуда
![]() .
.
Подставляя формулу (*) и извлекая корень, получаем ответ:
![]()


