Творческие копилки в математике

Технология работы

Пример (работа над понятием «одночлен»)

1

Дается определение математического объекта.

Одночленом называется алгебраическое выражение – произведение чисел и переменных, возведенных в степени с натуральными показателями.

2

Дети предлагают свои примеры объектов, подходящих под данное определение. Создается копилка.

Рассматривается как можно более широкий спектр чисел, переменных, степеней

3

Анализ копилки используется для изучения свойств объекта.

Вся собранная копилка выносится на доску. Выясняется, нет ли среди примеров ошибочных и проводится доказательство ( 7(x+y) не является одночленом, т. к. это произведение числа и суммы переменных, а не числа и степеней переменных. 41 является одночленом т. к. его можно представить в виде произведения чисел: 41= 41*1).

Замечание. Копилку можно разбивать на группы по основаниям, которые предлагают дети (одночлены с одной, двумя, тремя и т. п. переменными; одночлены, которые можно упростить, и неупрощаемые; одночлены, у которых числовой множитель стоит на первом месте…).

4

В некоторых случаях при классификации объектов выстраиваются новые определения.

Выстраивается определение стандартного одночлена. Можно составить копилку стандартных одночленов.

Технология работы

Пример (изучение свойств обыкновенной дроби в 5-м классе)

1

Рассматриваем математический объект с готовым определением. Учителем ставятся задачи на изменение объекта в рамках, допустимых определением.

Задача: изменять числитель дроби, сохраняя постоянным знаменатель.

2

Детьми осуществляются различные изменения объекта. Варианты изменений накапливаются.

Получаем дроби :

(у каждого ученика свой ряд). Дроби «прорисовываются».

3

Проводится совместный анализ полученной копилки (чаще всего в виде фронтальной работы в аудитории). При необходимости на этом этапе используются модели.

Дети замечают, что значение дроби становится больше с увеличением числителя.

4

Формулируются выявленные свойства объектов.

Формулируется свойство: с увеличением числителя значение дроби увеличивается.

5

Если возможно, полученные свойства доказываются.

В данном случае доказательство не проводится.

Технология работы

Пример (признаки параллелограмма)

1

Постановка задачи: «Известны определения и свойства математического объекта. Требуется найти признаки, по которым можно отличить данный объект среди других объектов более широкого множества».

Параллелограммом называется четырехугольник, противолежащие стороны которого попарно параллельны.

Свойства:

·        противолежащие стороны равны,

·        противолежащие углы равны,

·        диагонали точкой пересечения делятся пополам…

2

Учитель предлагает привести примеры объекта, совпадающего с данным по некоторым свойствам, но не относящегося к данному классу (не подходящему под определение). Собирается соответствующая копилка контрпримеров.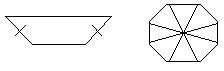

3

Копилка анализируется, выявляются признаки объекта.

Для того, чтобы четырехугольник стал параллелограммом, достаточно, чтобы две его противоположные стороны были параллельны и равны.

4

Признаки формулируются при помощи оборота «если…то».

Если в четырехугольнике две стороны параллельны и равны, то этот четырехугольник параллелограмм.

5

Признаки доказываются.

См. учебник «Геометрия – 8».

Технология работы

Пример (работа над понятием «равенство»)

1

Задаются элементы конструктора («части объекта»), предлагается составить с помощью данного конструктора объекты, соответствующие определению.

Элементы конструктора: числа, знаки арифметических действий, знаки операций сравнения, буквы-неизвестные. Задание: составить математические выражения.

2

Формируется копилка сконструированных объектов.

5+2=7; а>в; 3х-5=10; 25-11у+2х=0,2; ххх<8; …

3

Объекты объединяются в группы по наиболее ярким признакам. Анализируются способы получения новых объектов, соответствующих определению.

Группа равенств, группа неравенств, группа примеров, группа выражений без знаков сравнения, группа выражений не имеющих смысла, …

4

Выбирается группа для дальнейшей работы.

Выбираем равенства.

5

Копилка дополняется объектами выбранной группы.

Дополним копилку равенств.

6

Обсуждаются общие и новые (частные) приемы работы с объектом.

Повторяется работа с шага 3

Разбиваем копилку равенств на группы, выделяем группу равенств с переменными, называем ее уравнениями.

Технология работы

Примеры (задача № 10.247 из сборника задач под редакцией М.И.Сканави)

Задача: дано задание. Требуется отнести его к различным классам, выделяя свойства и признаки математических объектов.

Основания двух правильных треугольников со сторонами а и 3а лежат на одной прямой. Треугольники расположены по разные стороны от прямой и не имеют общих точек, а расстояние между ближайшими концами их оснований равно 2а. Найдите расстояние между вершинами треугольников, не принадлежащими данной прямой.

1

Собирается копилка признаков и свойств, пользуясь которыми можно работать с данным заданием.

·        ресурсы задачи:

·        стороны треугольников;

·        углы треугольников;

·        параллельные прямые;

·        секущие.

2

Определяются возможные способы решения поставленной задачи.

как можно найти длину отрезка:

·        по частям;

·        как стороны треугольников по теореме Пифагора;

·        как стороны подобных треугольников;

·        как стороны треугольников по теореме косинусов;

·        через площади;

·        целиком;

·        методом координат;

·        достроить до треугольника (несколько способов), найти его сторону по теореме косинусов или по теореме Пифагора;

·        достроить до параллелограмма (несколько способов), найти его сторону или диагональ;

·        …

3

Осуществляются решения разными способами.

4

Анализируются результаты.

5

Оцениваются разные способы решения задачи.

·        Самое быстрое решение – координатным методом.

·        Самое «простое» решение, но громоздкое – при помощи подобия по теореме Пифагора.

·        Самое «красивое» решение – по теореме косинусов, для достроенного треугольника.

Технология работы

Примеры «навыковых копилок»

1

Задаются элементы конструктора и условия работы с ними.

·        Рисунки из ломаных линий.

·        Рисунки из многоугольников.

·        Рисунки из окружностей.

·        Построение при помощи циркуля и линейки.

·        Телеграммы на числовом луче.

·        Рисунки в координатной плоскости.

2

Предлагается получить некоторый творческий продукт (загадку, рисунок и т. п.), используя заданные правила.

3

Создается выставка работ, обсуждаются качество их выполнения.